一生の短さについて

哲学的な考察はセネカに譲るとして、レイ・カーツワイル―加速するテクノロジー (NHK未来への提言)レイ カーツワイル (著), 徳田 英幸 (著)のあとがき（「インタビューを終えて」）の中に次のような興味深い一文がありました。

当時、大学のある先生の話した話の中に、「皆さんがＡ４サイズの方眼紙を１枚もっているとしましょう。我々が１日無事に暮らしたら１平方ミリを切り取ってみてください。もし、君たちが８０歳まで生きるとすると、君の一生を記録するのに何枚の方眼紙がいるでしょうか」という問いがあったのを覚えている。

Ａ４用紙のサイズは、210mm×297mmなので面積は62,370平方ミリです。

もし毎日１平方ミリずつ切り取っていくとすると、一生の間で切り取れるのは

　　１平方ミリ×３６５日×８０年＝29,200平方ミリ

となり、Ａ４用紙の半分も切り取れません。

上の引用文に続けて

なんと自分の一生を記録するのには、紙の半分以下しか必要ないのである。その先生は「皆さんの一生は、大変貴重な一生ですから、あまり無駄にしないように」という趣旨のことを言われたのが強く記憶に残っている。まさに、人の命がいかに短いかを可視化させられた瞬間であった。

私も全く同感です。

ところで、１日に１平方ミリを切り取るのではなく、１時間に１平方ミリ、１分間に１平方ミリ、１秒間に１平方ミリを切り取ればどうなるか、また１立方ミリならどうなるか、計算してみます。
切り取り作業に使える時間は、１日あたり１６時間としておきます。

１時間に１平方ミリ・１立方ミリ

１６時間×３６５日×８０年＝467,200平方ミリ＝$684^2$平方ミリ＝$78^3$立方ミリ

なので、一生を記録するために、用紙であれば約７０センチ四方の用紙、３次元の物体であれば一辺の長さが約８センチの物体が必要となります。

１分間に１平方ミリ・１立方ミリ

６０分×１６時間×３６５日×８０年＝28,032,000平方ミリ＝$5,295^2$平方ミリ＝$304^3$立方ミリ

なので、一生を記録するために、用紙であれば約５メートル四方の用紙、３次元の物体であれば一辺の長さが約３０センチの物体が必要となります。

１秒間に１平方ミリ・１立方ミリ

６０秒×６０分×１６時間×３６５日×８０年＝1,681,920,000平方ミリ＝$41,011^2$平方ミリ＝$1189^3$立方ミリ

なので、一生を記録するために、用紙であれば約４１メートル四方の用紙、３次元の物体であれば一辺の長さが約１２０センチの物体が必要となります。

一生の間、休むまもなく毎秒毎秒１立方ミリずつ削っていったとしても、一辺が１メートルちょっとの物体しか削り切ることができないというのは個人的には意外でした。

Google インフル トレンドの仕組み

Google インフル トレンドとは、インフルエンザ関連フレーズの検索数からインフルエンザの流行を予測するシステムで、報道でも取り上げられました。

インフルエンザ、ネット検索増えれば流行の兆し　米研究（朝日新聞　2008年12月12日9時13分）

【ワシントン＝勝田敏彦】
　　インフルエンザの季節、インターネットで関連の言葉が検索される件数を見ると、その流行がある程度予測できることが米国の研究でわかった。体の調子が悪くなった人が、医療情報をネットで探そうとすることを利用したもので、関連論文が相次いで発表された。

　　アイオワ大などのチームは、検索大手ヤフーと協力し、今年５月までの４年分の統計から関連語が検索される件数の推移を追った。すると、ウイルス検査で陽性反応が出始める１～３週間前、死者が増え始める５週間前ごろに、検索件数が急増していた。論文は１０月、米感染症専門誌（電子版）に発表された。

　　検索大手グーグルのチームも、米疾病対策センター（ＣＤＣ）と協力して同様の研究を行った。統計を取る検索語をうまく選ぶと、ＣＤＣが毎週発表している患者発生状況を１、２週間前に予測できるとしている。論文は１１月、英科学誌ネイチャー（電子版）に発表された。

インフルトレンドの予測結果（次の図）を見ると、高い精度でインフルエンザの流行を予測できているようです。


上のニュースでも述べられている通り、米疾病対策センター（ＣＤＣ）が患者発生状況のデータを発表するまでに、集計などで公表までに１、２週間かかっています。しかし、Google インフル トレンドでは１日遅れで流行予測ができます。

以降では、インフルトレンドではどのようにインフルエンザの流行を予測しているのかネイチャーの論文[Ginsberg,2008]をもとに計算方法の概要について紹介します。

モデル作成には次のデータを用います。

• 過去５年間（２００３年から２００８年）の数千億ものGoogle検索ログ
• 米国の地域（９つ）別にCDCが週単位で公表（流行期間のみ）した、インフルエンザ様疾患（ILI）*1で病院を訪れた外来患者数

まず、すべての検索フレーズのうち一般的な５千万種類のクエリー（検索フレーズ）を選びます。クエリーごとに検索数を週単位で合計し、それをその週の総検索数で割ることによりデータを標準化します。この値をクエリー比（query fraction）と呼びます。

インフルトレンドで採用された予測モデルは次の式です*2。
$$
\text{logit}(I(t)) = \alpha \text{logit} (Q(t)) + \epsilon
$$
ここで、

• $\alpha$：未知パラメータ
• $I(t)$：時間$t$のインフルエンザ様疾患（ILI）で病院を訪れた人の割合
• $Q(t)$：時間$t$のインフルエンザ様疾患（ILI）に関連するクエリー比
• $\epsilon$：誤差項
• $\text{logit}(p) = \log(p/(1-p))$

です。

後述するように、$I(t)$、$Q(t)$ともに過去のデータから得られますので、このモデル式に当てはめれば、未知パラメータ$\alpha$が求まり、モデルが決定されます。

$I(t)$、$Q(t)$の計算方法は次のとおりです。

通院割合$I(t)$の計算方法

CDCが週単位で公表（流行期間のみ）しているデータから計算できます。

クエリー比$Q(t)$の計算方法

５千万種類の検索フレーズごとのクエリー比$Q(t)$から上のモデル式をもとめ、モデルから予想される通院割合とCDCによる公式データとの相関係数を地域ごとに計算します*3。
地域ごとに得られた相関係数の平均*4をスコアとします。
検索フレーズごとのクエリー比の一例を図に示します*5。凡例の括弧内の数字はスコアの順位です。

ここまでは検索フレーズごとのクエリー比$Q(t)$を用いましたが、次のステップではスコアの高い上位$n$個の検索フレーズをひとまとめにして求めたクエリー比$Q(t)$と使ってモデルを作成します。そのモデルで予測された通院割合とCDCデータの相関を計算します。

その結果、スコアの高い上位４５個の検索フレーズ*6*7を用いると、モデルによる予測値と実際のデータとの相関係数が最も高くなることが分かりました。

このように作成したモデル（下図の黒線）と実際のインフルエンザ様疾患（ILI）患者割合（下図の赤線）を比べてみると両者がよく一致していることが分かります。

以上のように論文ではアメリカを９つに分けた地域ごとにインフルエンザ流行を予測するモデルについて述べられていますが、現在ではさらに細かい区分（州、都市）でインフルエンザ流行状況を提供しています。

インフルトレンドによる2009年新型インフルエンザ（A型H1N1亜型インフルエンザ）の予測については[Cook,2011]を、Yahooによるインフルエンザ予測については[Polgreen,2008]を、Yahoo Japanによる取り組みついても参考文献を参照してください。

参考文献：

Ginsberg, Jeremy, et al. "Detecting influenza epidemics using search engine query data." Nature 457.7232 (2008): 1012-1014.

Polgreen, Philip M., et al. "Using internet searches for influenza surveillance." Clinical infectious diseases 47.11 (2008): 1443-1448.

Cook, Samantha, et al. "Assessing Google flu trends performance in the United States during the 2009 influenza virus A (H1N1) pandemic." PLoS One 6.8 (2011): e23610.

“インフルエンザ”の患者数と検索数に高い関連性、「Yahoo!ビッグデータ」による分析

*1:1．突然の発症、2．38℃を越える発熱、3．上気道炎症状、4．全身倦怠感等の全身症状

*2:原著論文のSupplementary Informationによると、いろいろなモデルを試した結果、このシンプルなモデルで十分の予測可能であったとのこと

*3:米国の９つの地域ごとに、５千万種のクエリーそれぞれでモデルを作成するので、合計４億５千万個のモデルを作成することになります。これをGoogleの数百台のコンピュータで処理したとのこと。

*4:正確にはフィッシャーのZ変換$z = {1 \over 2}\ln\left({1+r \over 1-r}\right)$の平均

*5:原著論文のSupplementary Informationに相関データが公開されています。

*6:具体的な検索フレーズは非公開です。公開すると興味本位による検索によってインフルトレンドの有用性が低下してしまうためです。

*7:インフルエンザ流行時のメディア報道で検索フレーズとILI患者割合の相関が損なわれる可能性があったにもかかわらず、上位４５個のから得られた相関への影響はなかったとのこと。

Suica（スイカ）の利用履歴データから個人を特定できるのか

Business Media誠によるとJR東日本が7月1日より、IC乗車券「Suica」の利用履歴を外部に販売したとのこと。

　今回販売したのは、私鉄を含む首都圏約1800駅で、Suicaを利用して鉄道を乗り降りした履歴データ。JR東日本は、累積で約4300万件のSuicaを発行しているが、Suica定期券、My Suica（記名式）、Suicaカード（無記名）、モバイルSuicaすべての乗降履歴が対象だという。

　Suicaで鉄道に乗降した駅名と日時の履歴のだけでなく、記名式のSuicaやモバイルSuicaの場合は、年齢、性別も販売データに含まれる。一方、電子マネーとして利用した履歴や、利用者の氏名、電話番号はデータに含まれていない。

　Suicaには固有のIDがあるが、今回はSuicaのIDをそのまま渡すのではなく、異なるIDを振り直したと説明。そのIDごとに、乗車履歴年齢、性別のデータが分かる状態のデータを販売しているという。たとえば「No.0001：20歳の女性、7月7日10時10分にA駅で乗車、7月7日11時10分にB駅で下車、7月8日8時0分にC駅で乗車……」といった形のデータにまとまっているわけだ。

　「SuicaのIDにはひも付いていないから、個人が特定できるようにはなっていない。つまり、個人を特定できないので、（販売しているデータは）個人情報に当たらない」（広報部）

この記事によると、JR東日本はSuicaのIDを振り直したから履歴データから個人は特定できないと主張しているようです。
JR東日本のプレスリリース（Suica に関するデータの社外への提供について）に載っている図を見ると、一見特定はできなさそうです。

しかし、このように個人情報を匿名化すると本当に個人を特定できないのか、考えてみます。

まず、この匿名化されたSuica履歴データから、自分自身の情報を見つけられるのか考えてみます。

通勤通学でSuicaを毎日利用しているユーザーであれば、駅の乗降日時は自分自身で把握していますし、週末に出かけた先でSuicaを使えばその情報も自分が一番知っています。ある程度の期間でみると、自分と全く同じ行動を取る他人はまずいませんから、Suicaの利用履歴データから自分自身の行動に合致するデータを見つけ出すことは可能です。
自分の利用履歴を見つけられれば、それと同時に自分のSuicaの固有のIDと振り直されたIDの両方が手に入ることになります。
運が良ければ、固有IDと履歴データIDを関連付ける規則を推測できるかもしれません。
JR東日本がどのようにIDを変換しているかわかりませんが、もし、IDを乱数ではなくハッシュ関数で変換していたとしたら、ハッシュ関数が判明した時点で、固有IDと履歴データの全IDを一気に結びつけることができ、個人を特定できたも同然となってしまいます。

次に公開された情報をもとにその個人の履歴データを見つけ出せるか考えます。

たとえば、あるユーザーが自分のツイッターやFacebookに次のように書き込んだとします。

１月２日　３時４分　渋谷駅なう
...
５月６日　７時８分　舞浜駅（ディズニーランド）なう
...
９月１０日　１１時１２分　東京駅なう

この書き込みによりこのユーザーは自分の乗降の日付とおよその時間帯を他人に公表したことになります。たとえ駅の利用者が多くても、このユーザーと同じように駅を利用した人は非常に少ないはずです。さらに他の情報（乗降、年齢、生まれ月など）を追跡・加味し、これらの行動パターン・ユーザー属性をもとにSuicaの履歴データを検索すれば、このユーザーの行動パターンに合致するデータを見つけることが可能になります。
このようにSuica履歴データと出所が別の情報（ツイッター・Facebook・ブログなど）を突き合わせれば、個人の特定が可能となります。

上に挙げた例は単なる可能性だけの話ではなく、実際にアメリカで同じような出来事が起こっています。
ネットフリックスというオンラインDVDレンタル会社が、データ分析（レコメンドシステム精度向上）コンテスト用に顧客のレンタル利用データを公開しました。当然、個人情報は匿名化されていたため、このデータから個人は特定できないはずでした。しかし、ある研究者が、レンタル履歴の情報と、ネットフリックスとは関係のない映画情報サイトInternet Movie Database（IMD)に書き込まれた映画レビューとを付きあわせた結果、運悪く個人が特定されてしまいました。結果、このユーザーはネットフリックスを訴えました。
この詳しい経緯は匿名化した利用者データの公表が、なぜ、個人情報漏洩に？（2010年3月25日(木) 13時00分）がうまくまとまっていますので、詳しくはこちらを参照してください。

この有名なネットフリックスの事例からわかるように、データを匿名化していても個人を特定することは現実的に可能です。
しかし、JR東日本はデータを匿名化すれば個人を特定できないと考えているようであり、ビッグデータを販売する企業としては認識が低いと言わざるを得ません（といいますか「個人は特定できない」と断言するのは言いすぎではないかと思います）。
JR東日本のプレスリリース（Suica に関するデータの社外への提供についてよくいただくお問い合わせ）には、「提供先で他のデータと紐づけたり、目的以外の利用ができないよう契約で厳格に禁止しています。」と書かれていますが、契約は別にして、技術的に可能であれば個人が特定化されてしまうリスクは常にあります。

幸い、Suicaの利用履歴データは一般公開はされないようなので、データ流出事故が起きない限り、個人が特定されることはほぼ無いだろうと言えます。なので、それほど神経質になる必要はないのではないかと個人的には思います。

参考サイト

Netflix Spilled Your Brokeback Mountain Secret, Lawsuit Claims(WIRED)

$\int f(x)dg(x)$（リーマン＝スティルチェス積分）について

確率や統計の文献のなかで稀に
$$
a = \int f(x) dg(x)
$$
のような形（$dg(x)$の部分に注目）の積分が使われていて「？？？」となった方もいるかもしれません。$dg(x)$ではなく$dx$であれば、これは高校で習った積分
$$
a = \int f(x) dx
$$
になりお馴染みの形になりますが、$dg(x)$とは見慣れない形です。

実はこの積分は、リーマン＝スティルチェス積分（Riemann Stieltjes integral）と呼ばれ、リーマン積分（高校で習った積分の正式名）を拡張したものです*1。

この記事では、リーマン＝スティルチェス積分の定義と確率学への応用について簡単に紹介します。なお、数学的な厳密性については無視しています。

リーマン＝スティルチェス積分の定義

高校で習った積分の定義を少し一般化するとリーマン＝スティルチェス積分の定義になります。

定義を書く前に記号をいくつか用意しておきます。

• $f(x)$を区間$[a,b]$で有界な関数
• $g(x)$を区間$[a,b]$で単調増加する関数
• $P=\{x_0,x_1,\ldots,x_n\}$を区間$[a,b]$を分割したもの
• $m_i$を区間$[x_{i-1},x_i]$上での$f(x)$の下限（最小値とほぼ同じ意味）
• $M_i$を区間$[x_{i-1},x_i]$上での$f(x)$の上限（最大値とほぼ同じ意味）
• $\Delta g_i=g(x_i)-g(x_{i-1})$

このとき

• $$LS_P(f,g) = \sum_{i=1}^{n} m_i \Delta g_i$$
• $$US_P(f,g) = \sum_{i=1}^{n} M_i \Delta g_i$$

とすると、 $f(x)$の$g(x)$に関するリーマン＝スティルチェス積分$\int_{a}^{b} f(x) dg(x)$は
$$
\int_{a}^{b} f(x) dg(x)=\inf_{P} US_P(f,g) = \sup_{P} LS_P(f,g)
$$
で定義されます（$\inf, \sup$はそれぞれ$\min, \max$とほぼ同じ意味です）。高校で習った積分の定義に似ていますね。

このとき次の関係式
$$
\int_{a}^{b} f(x) dg(x)=\int_{a}^{b} f(x) g'(x)dx
$$
が成り立ちます。
この式により高校で習った積分（リーマン積分）とリーマン＝スティルチェス積分を関連付けることができます。

冒頭でリーマン＝スティルチェス積分はリーマン積分の拡張と書きましたが、この式を使って本当にそうなのか確かめてみます。
$g(x)=x$とおくと$g'(x)=1$になり、これを上の式に代入すれば
$$
\begin{align}
\int_{a}^{b} f(x) dg(x)&=\int_{a}^{b} f(x) g'(x) dx\\
&=\int_{a}^{b} f(x) dx
\end{align}
$$
となりますので、リーマン積分はリーマン＝スティルチェス積分で$g(x)=x$とした特別な場合に相当することがわかります。

確率論の応用

関数$h(x)$の期待値を数式で表現しようとすると、確率変数$X$が離散的な場合と連続な場合で次のように表現の仕方を変える必要があります。

• $X$が離散確率変数のとき：$E[h(X)]=\sum_{i=1}^{n} h(c_i) p(c_i)$（$p(x)$は確率分布関数）
• $X$が連続確率変数のとき：$E[h(X)]=\int_{-\infty}^{+\infty} h(x) f(x) dx$（$f(x)$は確率密度関数）

しかし、リーマン＝スティルチェス積分を使えば、確率変数$X$が離散的・連続的にかかわらず$h(x)$の期待値を
$$
E[h(X)]=\int_{-\infty}^{+\infty} h(x) dF(x)
$$
と一つの式で表現でき便利です。

確率変数$X$が連続の場合に上の式が成り立つことは簡単に示せます。

実際、$F(x)$を累積確率密度関数とすると$F'(x)=f(x)$なので
$$
\begin{align}
E[h(X)]&=\int_{-\infty}^{+\infty} h(x) f(x) dx\\
&=\int_{-\infty}^{+\infty} h(x) F'(x) dx\\
&=\int_{-\infty}^{+\infty} h(x) dF(x)
\end{align}
$$
となり上の期待値の式が成り立つことが示せました。

確率変数$X$が離散的な場合でも上の期待値の式が成り立つことが示せますが、数式が若干複雑になるので省略します。
興味のある方は参考文献を参照してください。

参考文献
Khuri, Andre I. Advanced calculus with applications in statistics. Vol. 486. Wiley. com, 2003.

*1:リーマン積分を拡張する方法は他にもいろいろあります。その中でもとくに重要なのがルベーグ積分です。実際のところ、ルベーグ積分の方がはるかに重要です。ちなみに、リーマン＝スティルチェス積分を一般化するとルベーグ＝スティルチェス積分となります。

乳幼児突然死症候群（SIDS）のリスク要因

乳幼児突然死症候群（Sudden Infant Death Syndrome、シッズ、以降 SIDS と略します）とは、「何の予兆もないままに、主に1歳未満の健康にみえた乳児に、突然死をもたらす疾患」（Wikipediaより）のことで、日本では1歳未満の乳児の死亡原因の第３位を占めています*1。
人口動態統計年報（２００９年）によると、SIDSによる死亡数は乳児１０万人あたり１３．６人ですので、約７０００人に１人の割合となります。

乳幼児突然死症候群（SIDS）を防止するための注意事項は母子健康手帳の副読本（P66～67、「眠り」の環境と注意ポイント）に書かれているそうですので参考になさってください。

SIDSのリスク要因およびリスク削減指針について調べたので、その内容を本記事にまとめました（基にした参考文献リストは本記事最後にあります）。

注意：本記事の正確性はまったく保証されていません。この記事で提供されている情報の使用や採用を試みた結果に対して責任を負うことはできません。本記事にもWikipedia:医療に関する免責事項と同様の免責事項が適用されるとします。

乳幼児突然死症候群による死者の月齢別割合

０歳児の月齢によってSIDSの死亡者数の割合がどのように変わるのか示したのが次の図です（文献[2]の図を改変）。
生後１ヶ月～２ヶ月で死亡者割合がピークに達しており、この時期は特に注意が必要なことが分かります。その後は１歳に近づくに連れて死亡者の割合が減少しています。

リスク要因

SIDSの高リスク要因と低リスク要因を図と表にまとめました（文献[1]参照）*2。
添い寝、柔らかな寝床、うつ伏せ寝のリスクが特に高いことがわかります。

リスク要因	リスク比	９５％信頼区間*3
添い寝（喫煙する母親）	13.9	9.58～20.09
妊娠３７週以下で出産	11.67	1.84～74.14
柔らかな寝床	5.1	3.1～8.3
うつ伏せ寝(あおむけ寝と比べて)	4.92	3.62～6.58
うつ伏せ寝（それ以外の姿勢と比べて）	4.3	3.39～5.39
添い寝（喫煙しない母親）	2.09	0.98～4.39
妊娠中の喫煙	2.03	1.16～3.54
親が無職	1.72	1.11～2.66
出生後にたばこの煙にさらされること	1.65	1.2～2.28
横向け寝（あおむけ寝と比べて）	1.36	1.03～1.8
予防接種	0.54	0.39～0.76
おしゃぶりの使用	0.39	0.31～0.5

乳幼児突然死症候群（SIDS）リスク削減指針

米国小児科学会（AAP、 American Academy of Pediatrics）が２０１１年に発表した乳幼児突然死症候群（SIDS）リスク削減指針（参考文献[3]）の一部を日本語に訳してみました（もちろん非公式ですし誤訳もあると思います）。
エビデンス（科学的根拠）の強さに応じてレベルＡからＣに分かれています。

エビデンスレベルＡの指針（しっかりした科学的根拠に基づく）

• １歳になるまでは、SIDSのリスクを減らすためにいつもあお向け寝で眠らせること。横向き寝は安全でないため薦められない。
• 固めの寝具を用いること。SIDSや窒息のリスクを減らすため、シーツでピッタリと覆われた固めのべビーベッドマットレスが推奨されます。
• 相部屋ですが添い寝はしないことが推奨されます。こうするとSIDSのリスクが５０％減ることがわかっています。さらに、大人のベッドで寝ている場合に起きる可能性がある窒息や首が絞まってしまうことを避けることができます。
• SIDS、窒息、首が絞まってしまうリスクを少なくするため、柔らかなもの（枕、枕のようなおもちゃ、キルト、掛け布団など）や畳んでいない寝具類（ブランケットやシーツ）はベビーベッドから遠ざけておくこと。
• 妊婦は定期的に妊婦検診を受けること。定期的に妊婦検診を受けた母親の乳児のSIDSリスクは低くなることが疫学的にわかっています。
• 妊娠中および出産後はタバコの煙を避けること。妊娠中の喫煙および乳児のいる環境にある煙草の煙は、ともにSIDSの主要なリスク因子です。
• 妊娠中および出産後のアルコールや違法ドラッグ摂取は避けること。出生前および出生後にアルコールや違法ドラッグに触れるとSIDSのリスクが増加します。
• 母乳で育てることが推奨されます。
• 昼寝や就寝時におしゃぶりをくわえさせることを検討すること。メカニズムはまだ不明ですが、おしゃぶりはSIDSに対して予防効果があることが報告されています。おしゃぶりが口から落ちても予防効果は就寝中持続します。
• 暑くし過ぎないこと。研究により暑くしすぎるとSIDSのリスクが増加することがわかっていますが、暑くしすぎること（overheating）の定義が研究によりまちまちです。したがって、適切な室温の指針を示すことは困難です。
• SIDSのリスクを低減する目的で家庭用心拍呼吸モニターを使用しないこと。
• SIDSのリスクを減らす全国的運動を拡大しましょう。（医療従事者向けの指針のため以降は略しました）

エビデンスレベルＢの指針（限定的または整合性に欠けた科学的根拠に基づく）

• 米国小児科学会および疾病対策予防センター（CDC）の推奨に従って乳児は予防接種を受けること。予防接種とSIDSの因果関係を示す証拠はありません。実際、最近の研究によると予防接種はSIDSに対する予防効果があることが報告されています。米国小児科学会の推奨に従って小児健診を受けること。
• SIDSのリスクを減らすための市販商品（wedgeやポジショナー、特殊マットレス、特殊寝具）は不要です。これらの商品がSIDSや窒息のリスクを軽減したり、商品自体の安全性に関する証拠はありません。
• 成長を促進するため、および斜頭症（positional plagiocephaly、フラットヘッド症候群）の発症を最小限にするために、監視下で、乳児が目覚めているときにうつぶせ寝の時間（tummy time、タミータイム）*4を持つことが推奨されます。

エビデンスレベルＣの指針（限定的または整合性に欠けた科学的根拠に基づく）

• 医療従事者、新生児室および新生児集中治療室のスタッフ、児童保育提供者は、SIDSリスク削減指針を出生直後から支持する必要があります。
• メディアやメーカーは、安全睡眠指針に反したメッセージングや広告を出すべきではありません。
• SIDSのリスク要因、原因、病態生理的メカニズムおよびその他の睡眠関連乳児死亡に関する研究・調査を、究極的には乳児死亡をゼロにすることを目標に、継続してください。

補足

詳細は文献[1]を参照してください。

最近の研究によると、乳児の死者の９２．２％でうつ伏せ寝、添い寝、べビーベッドやバシネット以外での就寝が原因であったことがわかっています。海外の事例ですが、１９９０年台からあお向け寝を推奨したところ、SIDSによる死亡数が５０～７０％も減少しました。

添い寝の禁止については賛否両論があります。添い寝の良い点は、授乳頻度が増えたり、親と子供の絆を形成したり、睡眠障害の減少があります。しかし、米国においてSIDSで死亡した乳児の約半数が添い寝によるものであるために、米国小児科学会は２００５年に添い寝を非推奨としました。
特に、低出生体重児、親が喫煙家、親が違法ドラッグや飲酒する場合に添い寝によるリスクが増大します。最近の研究によると、添い寝のリスクは４ヶ月以下の乳児で増加しますが、それ以降の乳児では明らかな増加は認められませんでした。
０歳児は親と別に、しかし、近くで、理想的には母親のそばのバシネットやべビーベッドで寝たほうがよい。また、ほかの子供と寝たり、親とカウチ（長椅子）やアームチェアで寝ることはすべきではありません。

あお向けで寝る習慣のある乳児の半数で斜頭症（positional plagiocephaly、フラットヘッド症候群）が見られ、あお向け寝の推奨以降はより頻繁に見られるようになりました。頭蓋骨の変形リスクを減少させるには、乳児が起きているときに、親の監視下でうつぶせ寝の時間（tummy time、タミータイム）を持つ必要があります。横向きで寝ている乳児では反対側に寝がえりさせることも必要です。
斜頸が見られるときは理学療法が役に立ちます。

乳幼児突然死症候群（SIDS）と似たものとして乳幼児突発性危急事態（Apparent Life-Threatening Events、ALTE、アルテ）がありますが、詳細はリンク先を参照してください。

参考文献

[1]．Adams, Stephen M., Matthew W. Good, and Gina M. DeFranco. "Sudden infant death syndrome." American Family Physician 79.10 (2009): 870-4.
[2]．Kattwinkel, J., et al. "The changing concept of sudden infant death syndrome: diagnostic coding shifts, controversies regarding the sleeping environment, and new variables to consider in reducing risk." Pediatrics 116.5 (2005): 1245-1255.
[3]．Moon, Rachel Y. "SIDS and other sleep-related infant deaths: expansion of recommendations for a safe infant sleeping environment." Pediatrics 128.5 (2011): e1341-e1367.

*1:ちなみに１位は「先天奇形，変形及び染色体異常」、２位は「周産期に特異的な呼吸障害等」、４位は「不慮の事故」となっています。

*2:図表のリスク比は正確にはオッズ比のことですが、専門的で一般の方にはわかりにくい用語なのでリスク比としました。

*3:詳しくは信頼区間を参照してください。

*4:tummyはおなか（ポンポン）という意味

Rでいろいろなカラーパレットをつかってグラフィックス表示してみた

Rにはrainbowをはじめとするいくつかのカラーパレットが標準で備わっており、これらを使えば十分綺麗なグラフィックスを作成することができます。
しかし、地図などの複雑なデータを表示したり、色覚異常の方でも色を識別できるような図を描きたい場合には標準のカラーパレットでは不十分なことがあります。そのような場合でも、あらたにパッケージをインストールすることで、多くのカラーパレットを使えるようになります。

使いたいパレットを選ぶときには、カラーバー（グラフィックス参考実例集：カラーパレット、グラフィックス参考実例集：RColorBrewer パッケージによるカラーパレットなど）やサンプル（デモ）を表示することが多いと思いますが、これらのシンプルな表示例だけでは複雑なデータでグラフィックス表示した場合にどうなるのか、イメージがつかめない場合があります。

そこで、複雑なデータにさまざまなカラーパレットを適用した例を作成しました。

R環境には、ニュージーランドのオークランドのMaunga Whau火山のデータ（volcano、10m×10m格子ごとの標高地形データ）が標準で含まれています。
これは比較的複雑なデータですので、これを用いて等高線図と3次元鳥瞰図をいろいろなカラーパレットで表示しました。

図の上方に表示されている「palette」がカラーパレット名、「package」がパッケージ名となります。

標準カラーパレット

colorRampsパッケージ

colorspaceパッケージ

dichromatパッケージ

RColorBrewerパッケージ

ワインの味（美味しさのグレード）は予測できるか？（２）

それでは実際に分析を行なっていきます。

分析方法

データ分析により、ワインの成分データから味のグレード（属性quality）を求めるモデルを作成します。
グレードqualityは０（とてもまずい）から１０（絶品）までの値をとる質的変数（順序尺度）とみなすのが原則ですが、分析の際には量的変数として扱います。

したがって回帰モデルを作成することによりデータを分析すれば良いことになります。用いた手法は、線形回帰モデル（交互作用あり・なし）、サポートベクター回帰（SVR、support vector regression）、ランダムフォレスト（random forest）です*1。

もちろん、グレードqualityを質的変数とみなすことにより、分類問題として分析することも可能です。実際は、あまり予測精度に違いはありませんでしたので結果は省略します。

また、事前につぎの処理をデータに施しておきます。

• 標準化
• 元データを2/3を訓練データに、1/3をテストデータに分割
• 外れ値の除去（LOF(local outlier factor)を用います）

この処理を施した結果、データサイズはつぎのようになりました。

ワイン	訓練データサイズ	テストデータサイズ
赤ワイン	1062	533
白ワイン	3263	1633

訓練データを用いてモデルを作成し、テストデータを用いて予測精度を評価します（教師あり学習です）。

ところで、モデルの予測結果は実数になるため、これを０から１０までの整数に変換する必要があります。この記事ではCortezら(2009)と同様な方法で整数に変換します。

$i$番目のテストデータのquality（正解のグレード）を$y_i$、予測結果（実数）を$\hat{y}_i$とします。このときqualityの予測クラス（整数で、予測グレードのこと）$p_i$はつぎの式で計算します。
$$
p_i =
\begin{cases}
y_i, & \text{if } |y_i - \hat{y}_i| \leqq T \\
\lfloor \hat{y}_i + 0.5 \rfloor, & \text{if } |y_i - \hat{y}_i| > T
\end{cases}
$$
ここで、$\lfloor x \rfloor$は床関数で、上の２番めの式は難しく見えますが、実際は単純な四捨五入のことです。

上の１番目の式に現れる$T$はしきい値で、０．５または１とします。それぞれの意味はつぎのとおりです。

• $T=0.5$のときは予測結果を四捨五入してqualityの予測クラスを求めます。
• $T=1$のときは予測結果と正解データの差が１以下であれば正解とみなします（すなわち評価が甘くなります）。

たとえば、正解が５、予測結果が５．８とすると、$T=0.5$のときは四捨五入して予測クラスは６となります。一方、$T=1$のときは正解と予測結果の差は０．８（＜１）なので予測クラスは（６ではなく）５となります。また、予測結果が６．１のばあいは、正解との差は１．１（＞１）なので、四捨五入して予測クラスは６となります。

$T=1$とすると評価基準が甘くなります。しかし、もともと味のグレードqualityは、３人以上のワイン査定人による評価結果の中間値を取ったものですので、正解のグレードと予測結果が１だけ異なっても正解とみなして問題ないと考えられます。

線形回帰モデル

まずはシンプルな線形回帰モデルでワインの味qualityを予測します。

まず属性間に多重共線性があるかどうか、VIF（分散拡大要因）を計算しました。

●赤ワイン
       fixed.acidity     volatile.acidity          citric.acid       residual.sugar            chlorides  free.sulfur.dioxide total.sulfur.dioxide              density                   pH            sulphates              alcohol 
            7.630214             1.790090             3.212295             1.687765             1.490558             2.061621             2.273877             5.993643             3.319835             1.402595             2.820069 
●白ワイン
       fixed.acidity     volatile.acidity          citric.acid       residual.sugar            chlorides  free.sulfur.dioxide total.sulfur.dioxide              density                   pH            sulphates              alcohol 
            3.260098             1.132510             1.151530            15.216226             1.242013             1.782381             2.323432            38.632377             2.469470             1.171794            11.087115 

白ワインのdensity、alcoholのVIFが１０を超えているため多重共線性を起こす可能性はありますが、ここでは全属性を用いて回帰モデルを作成します。

つぎに最適な重回帰モデルをステップワイズ法でモデル選択（AICで評価）しました。重回帰モデルの変数ごとの係数はつぎのとおりです。
なお、各変数の係数が本記事の冒頭で書いた式と異なるのは、データを標準化しているためです（冒頭に書いた式はわかりやすさのため標準化していないデータによる式です）。

●赤ワイン
Call:
lm(formula = .outcome ~ fixed.acidity + volatile.acidity + citric.acid + 
    residual.sugar + chlorides + free.sulfur.dioxide + total.sulfur.dioxide + 
    density + pH + sulphates + alcohol, data = data)

Residuals:
     Min       1Q   Median       3Q      Max 
 -2.34418 -0.38125 -0.04248  0.47055  2.11543 

Coefficients:
                      Estimate Std. Error t value Pr(>|t|)    
(Intercept)           5.617422   0.020111 279.317  < 2e-16 ***
fixed.acidity         0.029250   0.054355   0.538   0.5906    
volatile.acidity     -0.165753   0.027092  -6.118 1.33e-09 ***
citric.acid          -0.012419   0.035889  -0.346   0.7294    
residual.sugar        0.007935   0.026037   0.305   0.7606    
chlorides            -0.096093   0.023713  -4.052 5.45e-05 ***
free.sulfur.dioxide   0.064935   0.028752   2.258   0.0241 *  
total.sulfur.dioxide -0.143063   0.031568  -4.532 6.52e-06 ***
density              -0.022065   0.048730  -0.453   0.6508    
pH                   -0.084751   0.036164  -2.344   0.0193 *  
sulphates             0.159759   0.023963   6.667 4.21e-11 ***
alcohol               0.281640   0.033668   8.365  < 2e-16 ***
 ---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Residual standard error: 0.6543 on 1050 degrees of freedom
Multiple R-squared: 0.3413,     Adjusted R-squared: 0.3344 
F-statistic: 49.45 on 11 and 1050 DF,  p-value: < 2.2e-16 

●白ワイン
Call:
lm(formula = .outcome ~ fixed.acidity + volatile.acidity + citric.acid + 
    residual.sugar + chlorides + free.sulfur.dioxide + total.sulfur.dioxide + 
    density + pH + sulphates + alcohol, data = data)

Residuals:
    Min      1Q  Median      3Q     Max 
 -3.4069 -0.5082 -0.0447  0.4634  3.0696 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)           5.890e+00  1.322e-02 445.658  < 2e-16 ***
fixed.acidity         1.085e-01  2.337e-02   4.642 3.58e-06 ***
volatile.acidity     -1.924e-01  1.432e-02 -13.433  < 2e-16 ***
citric.acid           5.967e-05  1.397e-02   0.004 0.996592    
residual.sugar        5.205e-01  5.297e-02   9.825  < 2e-16 ***
chlorides            -2.557e-03  1.514e-02  -0.169 0.865939    
free.sulfur.dioxide   8.593e-02  1.819e-02   4.723 2.42e-06 ***
total.sulfur.dioxide -3.577e-03  2.026e-02  -0.177 0.859869    
density              -6.403e-01  8.385e-02  -7.636 2.93e-14 ***
pH                    1.324e-01  2.043e-02   6.481 1.05e-10 ***
sulphates             7.742e-02  1.457e-02   5.314 1.14e-07 ***
alcohol               1.604e-01  4.342e-02   3.694 0.000225 ***
 ---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Residual standard error: 0.7545 on 3251 degrees of freedom
Multiple R-squared: 0.2993,     Adjusted R-squared: 0.2969 
F-statistic: 126.2 on 11 and 3251 DF,  p-value: < 2.2e-16 

このモデルのもとでテストデータを用いてワインの味qualityを予測しました。予測結果の分割表はつぎのとおりです。なお、pred.halfは$T=0.5$の予測結果、pred.oneは$T=1$の予測結果です。

●赤ワイン
       pred.half
quality   4   5   6   7
      3   1   3   1   0
      4   0  10   3   0
      5   1 162  50   0
      6   0  62 151   8
      7   0   2  60  14
      8   0   0   4   1

       pred.one
quality   4   5   6   7
      3   1   3   1   0
      4   1   9   3   0
      5   0 207   6   0
      6   0   8 213   0
      7   0   2  22  52
      8   0   0   4   1

●白ワイン
       pred.half
quality   4   5   6   7
      3   1   2   4   1
      4   2  28  20   0
      5   2 203 293   9
      6   0 111 571  65
      7   0  10 195  74
      8   0   0  27  14
      9   0   0   0   1

       pred.one
quality   4   5   6   7   8
      3   1   2   4   1   0
      4  14  16  20   0   0
      5   0 423  75   9   0
      6   0   8 738   1   0
      7   0  10  63 206   0
      8   0   0  27  12   2
      9   0   0   0   1   0

結果をまとめるとつぎの表になります。

• 赤ワイン

しきい値T	正解率	精度（quality:4～7）	再現率（quality:3～8）
0.5	0.614	0.000 0.678 0.561 0.609	0.000 0.000 0.761 0.683 0.184 0.000
1	0.887	0.500 0.904 0.855 0.981	0.000 0.077 0.972 0.964 0.684 0.000

• 白ワイン

しきい値T	正解率	精度（quality:4～7）	再現率（quality:3～9）
0.5	0.521	0.400 0.573 0.514 0.451	0.000 0.040 0.400 0.764 0.265 0.000 0.000
1	0.847	0.933 0.922 0.796 0.896 1.000	0.000 0.280 0.834 0.988 0.738 0.049 0.000

正解率は、約５～６割（しきい値０．５）、約８～９割（しきい値１）です。

また、交互作用を考慮して線形回帰モデルを作成しましたが、予測性能は交互作用なしの場合とほぼ同じ（わずかによい）でしたので結果は省略します。

サポートベクターマシン（サポートベクター回帰）

$\epsilon$サポートベクター回帰で予測します。カーネルはRBF（パラメータは$\gamma$）を用いました。サポートベクターマシンについてはこちらを参照してください。

サポートベクター回帰にはいくつかのパラメータがありますので、最適なパラメータを５分割の交差検証で選択しました。探索したパラメータ空間は、$C \in \{2^{-5}, 2^{-4}, \ldots, 2^{5}\}, \gamma \in \{-15, -13, \ldots,3\}, \epsilon \in \{2^{-5}, 2^{-4}, \ldots, 2^{-1}\}$です。
最適なパラメータはつぎのとおりでした。

	$C$	$\gamma$	$\epsilon$
赤ワイン	1	0.125	0.25
白ワイン	2	0.125	0.25

このモデルのもとでテストデータを用いてワインの味qualityを予測しました。予測結果の分割表はつぎのとおりです。なお、pred.halfは$T=0.5$の予測結果、pred.oneは$T=1$の予測結果です。

●赤ワイン
       pred.half
quality   4   5   6   7
      3   1   4   0   0
      4   0  11   2   0
      5   0 177  36   0
      6   0  67 143  11
      7   0   3  50  23
      8   0   0   5   0

       pred.one
quality   4   5   6   7
      3   1   4   0   0
      4   1  10   2   0
      5   0 207   6   0
      6   0   1 220   0
      7   0   3  14  59
      8   0   0   5   0

●白ワイン
       pred.half
quality   4   5   6   7   8
      3   0   6   2   0   0
      4   8  32  10   0   0
      5   5 308 184  10   0
      6   2 150 526  69   0
      7   0   6 150 122   1
      8   0   2  11  27   1
      9   0   0   0   1   0

       pred.one
quality   4   5   6   7   8
      3   0   6   2   0   0
      4  22  18  10   0   0
      5   0 448  49  10   0
      6   2  15 726   4   0
      7   0   6  48 225   0
      8   0   2  11  22   6
      9   0   0   0   1   0

結果をまとめるとつぎの表になります。

• 赤ワイン

しきい値T	正解率	精度（quality:4～7）	再現率（quality:3～8）
0.5	0.644	0.000 0.676 0.606 0.676	0.000 0.000 0.831 0.647 0.303 0.000
1	0.914	0.500 0.920 0.891 1.000	0.000 0.077 0.972 0.995 0.776 0.000

• 白ワイン

しきい値T	正解率	精度（quality:4～8）	再現率（quality:3～9）
0.5	0.591	0.533 0.611 0.596 0.533 0.500	0.000 0.160 0.607 0.704 0.437 0.024 0.000
1	0.874	0.917 0.905 0.858 0.859 1.000	0.000 0.440 0.884 0.972 0.806 0.146 0.000

正解率は、約６割（しきい値０．５）、約９割（しきい値１）で、線形回帰モデルより予測結果が良いことが分かります。

ランダムフォレスト

ランダムフォレスト回帰で予測します。

このモデルのもとでテストデータを用いてワインの味qualityを予測しました。分割表はつぎのとおりです。なお、pred.halfは$T=0.5$の予測結果、pred.oneは$T=1$の予測結果です。

●赤ワイン
       pred.half
quality   4   5   6   7
      3   1   4   0   0
      4   0  11   2   0
      5   2 176  35   0
      6   0  54 154  13
      7   0   3  38  35
      8   0   0   3   2

       pred.one
quality   4   5   6   7   8
      3   1   4   0   0   0
      4   2   9   2   0   0
      5   0 209   4   0   0
      6   0   1 220   0   0
      7   0   3  11  62   0
      8   0   0   3   1   1

●白ワイン
       pred.half
quality   4   5   6   7   8
      3   0   4   4   0   0
      4   3  36  11   0   0
      5   0 346 156   5   0
      6   0 108 590  49   0
      7   0   2 125 152   0
      8   0   1   6  26   8
      9   0   0   0   1   0

       pred.one
quality   4   5   6   7   8
      3   0   4   4   0   0
      4  24  15  11   0   0
      5   0 457  45   5   0
      6   0   6 740   1   0
      7   0   2  27 250   0
      8   0   1   6  16  18
      9   0   0   0   1   0

結果をまとめるとつぎの表になります。

• 赤ワイン

しきい値T	正解率	精度（quality:4～7）	再現率（quality:3～8）
0.5	0.685	0.000 0.710 0.664 0.700	0.000 0.000 0.826 0.697 0.461 0.000
1	0.927	0.667 0.925 0.917 0.984 1.000	0.000 0.154 0.981 0.995 0.816 0.200

• 白ワイン

しきい値T	正解率	精度（quality:4～8）	再現率（quality:3～9）
0.5	0.673	1.000 0.696 0.661 0.652 1.000	0.000 0.060 0.682 0.790 0.545 0.195 0.000
1	0.912	1.000 0.942 0.888 0.916 1.000	0.000 0.480 0.901 0.991 0.896 0.439 0.000

正解率は、約７割（しきい値０．５）、約９割（しきい値１）で、線形回帰モデルやサポートベクターマシンより予測結果が良いことが分かります。

予測結果と正解の散布図（ジッターあり）を示します。

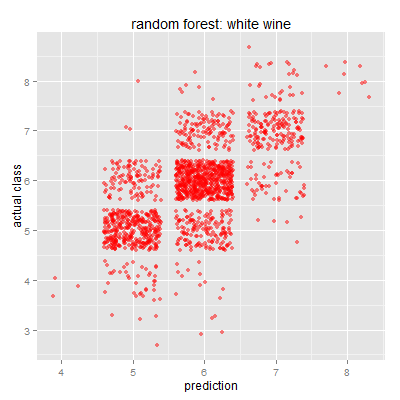
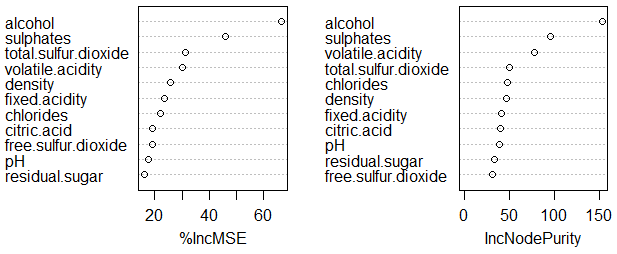
ランダムフォレストでは変数ごとの重要度を計算することができます。Cortezら(2009)の結果と異なるのですが、データを標準化したためと重要度の計算手法が異なるためと思われます。

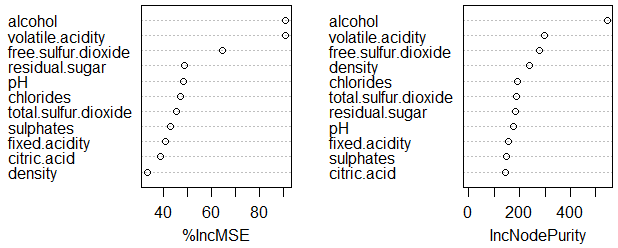
参考文献

Bache, K. & Lichman, M. (2013). UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science.

P. Cortez, A. Cerdeira, F. Almeida, T. Matos and J. Reis.
Modeling wine preferences by data mining from physicochemical properties.
In Decision Support Systems, Elsevier, 47(4):547-553. ISSN: 0167-9236.

*1:Cortezら(2009)が採用した手法は、線形回帰モデル、サポートベクター回帰、ニューラルネットワークです

ワインの味（美味しさのグレード）は予測できるか？（１）

データ分析の威力を色々な実例を挙げて述べた「その数学が戦略を決める」（イアン・エアーズ著）を読まれた方も多いと思います*1。

その中に、ワイン好きの経済学者オーリー・アッシェンフェルター（Orley Ashenfelter, プリンストン大学）がワインの質を計算する式

ワインの質 = 12.145＋0.00117 × 冬の降雨＋0.0614 × 育成期平均気温
　　　　　　－0.00386 × 収穫期降雨

により、伝統的なワイン批評家たちに「このやり方自体バカげていてまともには受け取れない」とまで言われたことが書かれています。

この式はワインの値段を予測する式ですが、ではワインの味を式で表すことは可能なのでしょうか？

実は可能で、ワインに含まれている成分（化学物質）の濃度などが分かれば、ワインの味（専門家が付けたグレード）を式で表すことができます。それが次の式です。
ちなみに、ワインの味（グレード）は、０（とてもまずい）から１０（絶品）まであります。

• 赤ワイン

ワインの味（グレード）＝0.026×(酒石酸濃度)－0.96×(酢酸濃度)
　　　　　　－0.10×(クエン酸濃度)＋0.014×(残留糖分濃度)
　　　　　　－2.3×(塩化ナトリウム濃度)＋0.0054×(遊離亜硫酸濃度)
　　　　　　－0.0041×(総亜硫酸濃度)－17×(密度)－0.50×(ｐＨ)
　　　　　　＋0.91×(硫酸カリウム濃度)＋0.26×(アルコール度数)＋22

• 白ワイン

ワインの味（グレード）＝0.13×(酒石酸濃度)－1.9×(酢酸濃度)
　　　　　　－0.0050×(クエン酸濃度)＋0.10×(残留糖分濃度)
　　　　　　－0.12×(塩化ナトリウム濃度)＋0.0048×(遊離亜硫酸濃度)
　　　　　　＋0.000076×(総亜硫酸濃度)－210×(密度)＋0.86×(ｐＨ)
　　　　　　＋0.68×(硫酸カリウム濃度)＋0.14×(アルコール度数)＋209

ワインの成分さえ分かれば、ワイン専門家による評価の代わりに、この式を使ってワインの味を数値的に求めることができます。実際、この式の予測精度は約５～６割です。後述しますがより高度な手法を使えば精度は約７割となります（グレードをピタリと予測するのではなくグレード±１までなら正解とすれば正解率は約９割になります）。

さらには、この式を使えばどの成分を増やせばまたは減らせばワインをより美味しくできるかがわかります。
実際、これらの成分の中にはワインの製造過程でコントロールできるものがあります。たとえば、収穫前のぶどうの糖度をモニターすることによりワインのアルコール度数を高くしたり低くしたりできますし、残留糖分は、イースト菌（酵母菌）による糖の発酵を一時的に止めることで増やすことができます。

それでは、次からワインの成分から味（グレード）を予測するデータ分析の方法について述べます。

ワインのデータについて

データはUCI Machine Learning Repository（Wine Quality Data Set）から入手できます。

このデータは、ポルトガルワインの一種である、西北端の大西洋に面するミーニョ(Minho)地方で作られたヴィーニョ・ヴェルデ（Vinho Verde）を測定したデータから構成されています。

データセットは赤ワインと白ワインの２種類のデータ群から構成されており、ワイン（銘柄名は不明）ごとに測定された１１種類の成分データとそのワインの味を評価したグレード（数値）からなっています。なお、グレードは３人以上のワイン査定士が評価した結果の中間値です（グレードは０（とてもまずい）から１０（絶品）まで）（詳細はCortezら(2009)を参照してください）。
データサイズはそれぞれ1599、4898です。変数一覧はつぎのとおりです。

属性（単位）	英語表記
ワインの味（グレード）	quality; from 0 (very bad) to 10 (excellent)
酒石酸濃度（$g/dm^3$）	fixed acidity ($g$(tartaric acid)/$dm^3$)
酢酸濃度（$g/dm^3$）	volatile acidity ($g$(acetic acid)/$dm^3$)
クエン酸濃度（$g/dm^3$）	citric acid ($g/dm^3$)
残留糖分濃度（$g/dm^3$）	residual sugar ($g/dm^3$)
塩化ナトリウム濃度（$g/dm^3$）	chlorides ($g$(sodium chloride)/$dm^3$)
遊離亜硫酸濃度（$mg/dm^3$）	free sulfur dioxide ($mg/dm^3$)
総亜硫酸濃度（$mg/dm^3$）	total sulfur dioxide ($mg/dm^3$)
密度（$g/dm^3$）	density ($g/dm^3$)
pH	pH
硫酸カリウム濃度（$g/dm^3$）	sulphates ($g$(potassium sulphate)/$dm^3$)
アルコール度数（% vol.）	alcohol (% vol.)

今後は、基本的に英語表記の属性名を用います。

各種記述統計量は次のとおりです。

• 赤ワイン

                     nobs NAs Minimum   Maximum 1. Quartile 3. Quartile      Mean   Median       Sum  SE Mean  LCL Mean  UCL Mean    Variance     Stdev Skewness  Kurtosis
fixed.acidity        1599   0 4.60000  15.90000      7.1000    9.200000  8.319637  7.90000 13303.100 0.043541  8.234234  8.405041    3.031416  1.741096 0.980908  1.119699
volatile.acidity     1599   0 0.12000   1.58000      0.3900    0.640000  0.527821  0.52000   843.985 0.004478  0.519037  0.536604    0.032062  0.179060 0.670333  1.212689
citric.acid          1599   0 0.00000   1.00000      0.0900    0.420000  0.270976  0.26000   433.290 0.004872  0.261420  0.280531    0.037947  0.194801 0.317740 -0.793046
residual.sugar       1599   0 0.90000  15.50000      1.9000    2.600000  2.538806  2.20000  4059.550 0.035259  2.469646  2.607965    1.987897  1.409928 4.532140 28.485020
chlorides            1599   0 0.01200   0.61100      0.0700    0.090000  0.087467  0.07900   139.859 0.001177  0.085158  0.089775    0.002215  0.047065 5.669694 41.525963
free.sulfur.dioxide  1599   0 1.00000  72.00000      7.0000   21.000000 15.874922 14.00000 25384.000 0.261586 15.361835 16.388009  109.414884 10.460157 1.248222  2.007221
total.sulfur.dioxide 1599   0 6.00000 289.00000     22.0000   62.000000 46.467792 38.00000 74302.000 0.822640 44.854225 48.081360 1082.102373 32.895324 1.512689  3.785676
density              1599   0 0.99007   1.00369      0.9956    0.997835  0.996747  0.99675  1593.798 0.000047  0.996654  0.996839    0.000004  0.001887 0.071154  0.922500
pH                   1599   0 2.74000   4.01000      3.2100    3.400000  3.311113  3.31000  5294.470 0.003861  3.303540  3.318686    0.023835  0.154386 0.193320  0.795919
sulphates            1599   0 0.33000   2.00000      0.5500    0.730000  0.658149  0.62000  1052.380 0.004239  0.649834  0.666463    0.028733  0.169507 2.424118 11.661529
alcohol              1599   0 8.40000  14.90000      9.5000   11.100000 10.422983 10.20000 16666.350 0.026650 10.370710 10.475256    1.135647  1.065668 0.859214  0.191659
quality              1599   0 3.00000   8.00000      5.0000    6.000000  5.636023  6.00000  9012.000 0.020196  5.596410  5.675635    0.652168  0.807569 0.217393  0.287915

• 白ワイン

                     nobs NAs Minimum   Maximum 1. Quartile 3. Quartile       Mean    Median        Sum  SE Mean   LCL Mean   UCL Mean    Variance     Stdev Skewness  Kurtosis
fixed.acidity        4898   0 3.80000  14.20000    6.300000      7.3000   6.854788   6.80000  33574.750 0.012058   6.831149   6.878426    0.712114  0.843868 0.647355  2.166627
volatile.acidity     4898   0 0.08000   1.10000    0.210000      0.3200   0.278241   0.26000   1362.825 0.001440   0.275418   0.281065    0.010160  0.100795 1.576014  5.081904
citric.acid          4898   0 0.00000   1.66000    0.270000      0.3900   0.334192   0.32000   1636.870 0.001729   0.330801   0.337582    0.014646  0.121020 1.281135  6.163631
residual.sugar       4898   0 0.60000  65.80000    1.700000      9.9000   6.391415   5.20000  31305.150 0.072473   6.249336   6.533494   25.725770  5.072058 1.076434  3.462415
chlorides            4898   0 0.00900   0.34600    0.036000      0.0500   0.045772   0.04300    224.193 0.000312   0.045160   0.046384    0.000477  0.021848 5.020254 37.508493
free.sulfur.dioxide  4898   0 2.00000 289.00000   23.000000     46.0000  35.308085  34.00000 172939.000 0.243009  34.831679  35.784491  289.242720 17.007137 1.405883 11.447515
total.sulfur.dioxide 4898   0 9.00000 440.00000  108.000000    167.0000 138.360657 134.00000 677690.500 0.607239 137.170196 139.551119 1806.085491 42.498065 0.390471  0.568587
density              4898   0 0.98711   1.03898    0.991723      0.9961   0.994027   0.99374   4868.746 0.000043   0.993944   0.994111    0.000009  0.002991 0.977174  9.777368
pH                   4898   0 2.72000   3.82000    3.090000      3.2800   3.188267   3.18000  15616.130 0.002158   3.184037   3.192496    0.022801  0.151001 0.457502  0.527568
sulphates            4898   0 0.22000   1.08000    0.410000      0.5500   0.489847   0.47000   2399.270 0.001631   0.486650   0.493044    0.013025  0.114126 0.976595  1.586208
alcohol              4898   0 8.00000  14.20000    9.500000     11.4000  10.514267  10.40000  51498.880 0.017584  10.479795  10.548739    1.514427  1.230621 0.487044 -0.699877
quality              4898   0 3.00000   9.00000    5.000000      6.0000   5.877909   6.00000  28790.000 0.012655   5.853101   5.902718    0.784356  0.885639 0.155701  0.213767

属性ごとの箱ひげ図は次のとおりです。

• 赤ワイン

• 白ワイン

ワインの味（グレードquality）のヒストグラムはつぎのとおりです。グレードは０から１０までの値を取ることができますが、このワインデータに含まれているサンプルには、３～８（赤ワイン）、３～９（白ワイン）のデータしかないことがわかります。

それでは実際に分析を行なっていきます*2。

*1:訳書では「super crunchers」を「絶対計算者」と訳していますが訳語に非常に違和感を感じます。本書で取り上げられている人達は統計的・確率的手法で分析しているため「絶対」とは真逆だと思うからです。今流行のデータサイエンティストと訳したほうがいいのではないかと思います。

*2:当初、属性residual.sugar, chlorides, free.sulfur.dioxide, total.sulfur.dioxide, sulphatesについてはlog変換した属性を用いたのですが、変換前よりわずかに精度が良くなるだけでしたのでlog変換しないときの結果のみを示します

TOEICのスコア分布は正規分布に従っているのか

TOEICの公式ホームページのTOEICの平均スコア・スコア分布から各実施回の「平均スコア」ページを見ると、「■注意」欄に「すべてのスコアが正規分布しているという仮説に従えば、」と書かれています。

ほんとうにTOEICスコアは正規分布に従っているという仮説が正しいのか調べてみました。

実施回ごとに平均と標準偏差が公表されていますので、このデータを使って正規分布のグラフを描くことができます。
第177回（2013年1月)[受験者数：106,477人]の場合で、実際の得点分布とスコアが正規分布に従うと仮定したときの得点分布を描いたのが下図です。

図からわかるように、実際のTOEICスコアと正規分布は乖離していますので、スコアの分布は正規分布に従わないと言えます。

念の為に正規性の検定（Shapiro-Wilk検定、Kolmogorov-Smirnov検定）を行ったところ、有意確率p<0.001で帰無仮説が棄却されました。すなわち、上と同様の結論、実際のTOEICスコア分布は正規分布に従わないことがわかりました。

TOEICで満点（９９０点）を取った人は何人か？

TOEICで満点のスコアである９９０点を取った人は何人いるのか気になったので、その人数を推定してみました。

TOEICの公式ホームページでTOEICの平均スコア・スコア分布が公開されており、そのページを見ればスコア区分（５０点刻み）ごとの人数はわかります。しかし、不思議なことに８９５から満点の９９０点までは刻み幅が９５に拡大されており、ここだけデータの間隔が粗くなっています。そのため、このスコア分布をただ見ただけでは満点（９９０点）を取った人が何人いるのか見当がつきません。

もし最低スコア１０点から最高スコア９９０点まで、スコアごと（５点刻み）の人数が推定できれば、満点を取った受験者数を推定することができます。

TOEICは頻繁に実施されています。どの実施回のデータを分析対象にしても良いのですが、この記事では第177回（2013年1月)[受験者数：106,477人]のTOEICスコアを分析対象にします。

スコアごとの人数推定

とりあえず参考までに公開されているTOEICのスコア分布（トータルスコアとリスニング・リーディングスコア区分ごとの人数）のグラフを見ておきます。

さて、公開されているスコア分布表にはスコア区分ごとの人数しか書かれていないので、この表からスコアごとの人数までは当然ながらわかりません。しかし、後述する方法によりこのデータだけから１０～９９０まで５刻みでスコアごとの人数を推定しました。
下図がそのグラフです。横軸はスコアで、縦軸はそのスコアを取った受験者の推定人数を表しています。
スコアごとの人数の一覧表は参考までに後半に載せておきました。

図からわかるように、満点スコア９９０のところでいきなり人数が急増しています。一見すると９９０だけ振る舞いが異なるため計算間違いのように思えますが、次のように考えればこの結果は合理的と考えられます。

まず、９９０より低いスコア（たとえば８００）の場合で考えると、そのスコアの人数が意味することは、スコアちょうどの英語力を持っている受験者がその人数だけいるということです。
しかしスコア９９０の場合には人数の意味する内容が異なると考えられます。９９０を取った受験者の内訳を想像してみると、９９０ちょうどの実力を持っている人もいれば、９９０を遥かに超える英語力を持っていても、TOEICの満点９９０を超えるスコアを取ることは不可能なので結果的に９９０となった人もいます。すなわち、スコア９９０の人数には９９０以上の英語力を持った受験者すべてが含まれていることになるため、９９０の人数が急増したと考えられます*1。

問題のスコア９９０を達成した受験者の人数ですが、後述するスコア別推定人数の一覧表をみると、満点９９０を達成した人は全受験者の０．３３％と推測されます。
実際、TOEIC 全国公開試験で満点 990 を獲得せよによると、

第１０５回（２００４年３月）全国公開試験において受験者の何人が 990 満点を獲得したかは、990 満点を獲得した受験者のスコアレポートに記載されている Percentile Rank の数字で推測できます。過去の公開試験では、この数字が 99.7 / 99.8 / 99.9 / 100.0 のことがありました。

とのことで、９９０を獲得した人の割合は０．３％から０．０％であったことがわかります。この数字は本記事での推定割合０．３３％と非常に近いので、スコア別人数推定値は案外いい線いっていると思います。
ちなみに、この引用文にあるPercentile Rank（パーセンタイルランク）とは、下位者100分比（％）のことで、そのスコアに満たない受験者が占める割合（％）を表しています。たとえば、９９０のPercentile Rankが９９．７とすると９９０の人の割合は全受験者の０．３％（＝１００－９９．７）となります。Percentile Rankの詳細については、公開テスト 平均スコア・スコア分布一覧の「スコア分布」ページの「■注意」を御覧ください。

さて、上の図は最小スコア間隔（５刻み）で最も細かいグラフでした。次に示す図は３０点、４０点、５０点ごとに人数を集計したグラフです。スコア区分で集計することにより、グラフが９９０までなめらかにつながって見えます。

次の図はスコア区分をTOEICの公式データと同じにして推定値を集計したグラフです。全体的に公表値と推定値がよく一致していることが分かります。

第177回 TOEICスコアごとの推定人数一覧表

参考データとして、第177回（2013年1月)でのTOEICスコアごとの人数とその下位者100分比（％）の推定値一覧表を示します。

スコア	人数（推定値）	下位者100分比（％）（推定値）
10	3	0
15	1	0
25	1	0
30	1	0
35	1	0.01
40	1	0.01
45	1	0.01
50	1	0.01
55	1	0.01
60	1	0.01
65	2	0.01
70	1	0.01
75	3	0.01
80	3	0.02
85	3	0.02
90	3	0.02
95	4	0.03
100	6	0.03
105	6	0.04
110	7	0.04
115	10	0.05
120	9	0.06
125	14	0.07
130	18	0.08
135	19	0.1
140	23	0.11
145	28	0.14
150	29	0.16
155	35	0.19
160	39	0.22
165	45	0.26
170	52	0.3
175	56	0.35
180	68	0.4
185	81	0.47
190	89	0.54
195	92	0.63
200	109	0.71
205	115	0.82
210	124	0.92
215	143	1.04
220	163	1.17
225	173	1.33
230	185	1.49
235	200	1.66
240	229	1.85
245	237	2.07
250	252	2.29
255	274	2.53
260	293	2.78
265	312	3.06
270	346	3.35
275	368	3.68
280	375	4.02
285	399	4.37
290	415	4.75
295	449	5.14
300	471	5.56
305	495	6
310	521	6.47
315	557	6.96
320	552	7.48
325	582	8
330	608	8.55
335	622	9.12
340	655	9.7
345	687	10.32
350	697	10.96
355	751	11.62
360	753	12.32
365	782	13.03
370	790	13.76
375	821	14.5
380	830	15.28
385	844	16.05
390	855	16.85
395	888	17.65
400	907	18.48
405	920	19.34
410	937	20.2
415	954	21.08
420	957	21.98
425	971	22.87
430	981	23.79
435	1001	24.71
440	1019	25.65
445	1018	26.6
450	1028	27.56
455	1019	28.53
460	1034	29.48
465	1053	30.46
470	1056	31.44
475	1051	32.44
480	1050	33.42
485	1059	34.41
490	1065	35.4
495	1082	36.4
500	1070	37.42
505	1074	38.43
510	1081	39.43
515	1077	40.45
520	1076	41.46
525	1074	42.47
530	1088	43.48
535	1075	44.5
540	1079	45.51
545	1076	46.52
550	1082	47.53
555	1064	48.55
560	1072	49.55
565	1076	50.55
570	1036	51.56
575	1049	52.54
580	1050	53.52
585	1058	54.51
590	1047	55.5
595	1024	56.49
600	1040	57.45
605	1024	58.42
610	1006	59.39
615	991	60.33
620	993	61.26
625	986	62.2
630	993	63.12
635	965	64.05
640	946	64.96
645	944	65.85
650	914	66.73
655	918	67.59
660	922	68.46
665	899	69.32
670	881	70.17
675	891	70.99
680	853	71.83
685	851	72.63
690	844	73.43
695	838	74.22
700	810	75.01
705	798	75.77
710	796	76.52
715	780	77.27
720	771	78
725	758	78.72
730	748	79.44
735	730	80.14
740	711	80.82
745	729	81.49
750	711	82.18
755	688	82.84
760	679	83.49
765	673	84.13
770	664	84.76
775	639	85.38
780	632	85.98
785	616	86.58
790	620	87.16
795	605	87.74
800	582	88.31
805	579	88.85
810	571	89.4
815	557	89.93
820	528	90.46
825	529	90.95
830	514	91.45
835	499	91.93
840	494	92.4
845	478	92.87
850	447	93.31
855	437	93.73
860	415	94.14
865	402	94.53
870	393	94.91
875	374	95.28
880	358	95.63
885	342	95.97
890	329	96.29
895	307	96.6
900	294	96.89
905	273	97.16
910	261	97.42
915	241	97.66
920	221	97.89
925	202	98.1
930	189	98.29
935	172	98.46
940	159	98.63
945	146	98.78
950	134	98.91
955	128	99.04
960	115	99.16
965	105	99.27
970	93	99.37
975	86	99.45
980	77	99.53
985	67	99.61
990	351	99.67
合計	106,475	-

上の表の下位者100分比（％）をグラフしたものが下図です。

ところで、公式ページの公開テスト 平均スコア・スコア分布一覧の「平均スコア」ページにはトータルスコアの平均と標準偏差が載っています。この数字と推定値と比較すると、両者がほぼ一致することがわかります。

	公表値	推定値
平均スコア	570.3	567.8
標準偏差	174.0	176.9

スコアごとの人数推定方法

スコアごとの人数をどのように推定したか、概要を書いておきます。

用いたデータはTOEICスコア分布の公表値のみ。
手順は次のとおりです。

• スコア区分ごとの人数データからカーネル密度推定により滑らかな推定スコア分布を求めます。
• 推定スコア分布にしたがう乱数を生成することにより、受験者ごとの推定スコア（０から１１００まで）を計算します。
• 推定スコアを集計します。ただし、推定スコアが９９５以上となった人のスコアは９９０とみなして集計します（下図）。

*1:WikipediaによるとTOEICの採点方法は普通のテストとは異なるので９９０での振る舞いは本記事の推測と異なるかもしれません。